题目内容
(本小题满分14分) 如果对于函数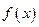 的定义域内的任意
的定义域内的任意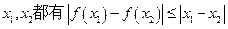 成立,那么就称函数
成立,那么就称函数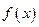 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数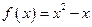 ,
,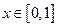 是否是 “平缓函数”?
是否是 “平缓函数”?
(2)若函数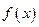 是闭区间
是闭区间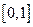 上的“平缓函数”,且
上的“平缓函数”,且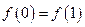 .证明:对任意的
.证明:对任意的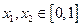 都有
都有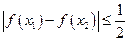 .
.
(1)对于任意

 ,
,
(



(2)当 时,由已知得
时,由已知得
当
 ,其中
,其中




故对于任意 都有
都有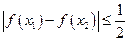 成立.
成立.
解析

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
题目内容
(本小题满分14分) 如果对于函数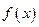 的定义域内的任意
的定义域内的任意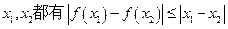 成立,那么就称函数
成立,那么就称函数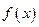 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数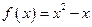 ,
,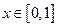 是否是 “平缓函数”?
是否是 “平缓函数”?
(2)若函数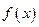 是闭区间
是闭区间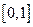 上的“平缓函数”,且
上的“平缓函数”,且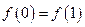 .证明:对任意的
.证明:对任意的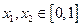 都有
都有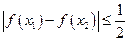 .
.
(1)对于任意

 ,
,
(



(2)当 时,由已知得
时,由已知得
当
 ,其中
,其中




故对于任意 都有
都有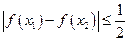 成立.
成立.
解析

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案