题目内容
【题目】已知![]() 中,边
中,边![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,![]() ,过
,过![]() 边上一点
边上一点![]() (异于端点)引边
(异于端点)引边![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,再由
,再由![]() 引边
引边![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,又由
,又由![]() 引边
引边![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,同样的操作连续进行,得到点列
,同样的操作连续进行,得到点列![]() 、
、![]() 、
、![]() ,设
,设![]() (
(![]() );
);
(1)求![]() ;
;
(2)结论“![]() ”是否正确?请说明理由;
”是否正确?请说明理由;
(3)若对于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
【答案】(1)![]() ;(2)正确;见解析(3)
;(2)正确;见解析(3)![]() ;
;
【解析】
(1)根据平面向量的模长公式与数量积运算法则,求出![]() ;
;
(2)结论正确,由余弦定理,结合平面向量的线性表示与坐标表示,求出![]() ;
;
(3)画出图形,结合图形,得出![]() 与
与![]() 的关系,即
的关系,即![]() 构成一个等比数列,求出
构成一个等比数列,求出![]() 的表达式,再根据题意求出
的表达式,再根据题意求出![]() 的取值范围.
的取值范围.
(1)![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]()
![]() ,
,
![]() ;
;
(2)结论正确,由(1)知,![]() ,
,![]() ,
,![]() ;
;
由余弦定理得![]() ;
;
又![]() ,
,
则![]() ,
,
则![]() ,
,
所以,![]() ;
;
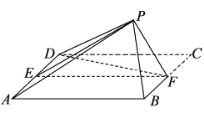
(3)画出图形,如图所示,结合图形,可得![]() ,则
,则![]() ,
,
![]() 构成一个等比数列,公比为
构成一个等比数列,公比为![]() ,
,
 ,
,
![]() ,又
,又![]() ,
,
![]() 的取值范围是
的取值范围是![]() .
.


练习册系列答案
相关题目