题目内容
若函数f（x）=
的定义域为R，则实数m的取值范围是________．
0≤m≤1
分析：利用该函数的被开方数大于等于零得出该函数有意义需满足的不等式，结合恒成立问题得出字母m满足的不等式
解答：依题意，当x∈R时，mx2-6mx+m+8≥0恒成立．
当m=0时，x∈R；
当m≠0时，
即
，解之得0＜m≤1．
故答案为0≤m≤1．
点评：本题考查偶次根式的定义域的求解，考查不等式恒成立问题的解决办法，关键要进行等价转化．
分析：利用该函数的被开方数大于等于零得出该函数有意义需满足的不等式，结合恒成立问题得出字母m满足的不等式
解答：依题意，当x∈R时，mx2-6mx+m+8≥0恒成立．
当m=0时，x∈R；
当m≠0时，
即，解之得0＜m≤1．故答案为0≤m≤1．
点评：本题考查偶次根式的定义域的求解，考查不等式恒成立问题的解决办法，关键要进行等价转化．
练习册系列答案
相关题目
．
．
与
的大小，并说明你的理由．
．
．
与
的大小，并说明你的理由．
．
．
与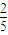
的大小，并说明你的理由．