Question

(本小题满分12分)

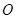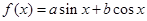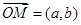已知为坐标原点，对于函数，称向量为函数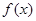的伴随向量，同时称函数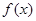为向量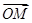的伴随函数．

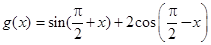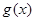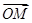（Ⅰ）设函数，试求的伴随向量的模；

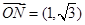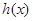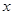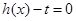（Ⅱ）记的伴随函数为，求使得关于的方程在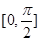内恒有两个不相等实数解的实数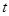的取值范围．

 

Answer 1

【答案】

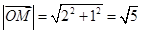(1) (2)

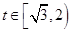
【解析】

试题分析：解：（Ⅰ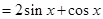）∵，  ……………… 2分

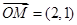∴．               ………………………… 4分

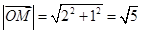故.        ……………………… 5分

（Ⅱ）由已知可得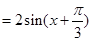，……………………… 7分

∵， ∴，

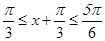故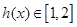.        ……………………… 9分

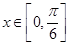∵当时，函数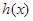单调递增，且；

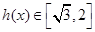当时，函数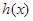单调递减，且.

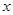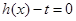∴使得关于的方程在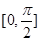内恒有两个不相等实数解的实数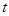的取值范围为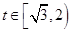．    … 12分

考点：三角函数性质，向量数量积，函数与方程。

点评：需要熟练运用三角函数的性质求解值域，单调区间，考查化归与转化思想、函数与方程思想、数形结合思想以及分类与整合思想等，属于中档题。