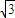题目内容
a2+b2=1,b2+c2=2,c2+a2=2,则ab+bc+ca的最小值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
分析:先把题设中的三个等式联立可求得a,b和c,再把它们的值代入所求代数式,即可得解.
解答:解:∵b2+c2=2,c2+a2=2,
∴b2+c2=c2+a2
∴b2=a2
又a2+b2=1,
所以当a=b=
,
c=-
时ab+bc+ca有最小值为:
×
+
×(-
)+
×(-
)=
-
,
ab+bc+ca的最小值为
-
,
故选B.
∴b2+c2=c2+a2
∴b2=a2
又a2+b2=1,
所以当a=b=
| ||
| 2 |
c=-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
ab+bc+ca的最小值为
| 1 |
| 2 |
| 3 |
故选B.
点评:本题解题的关键是通过已知条件求得a,b和c值,然后代入即可.

练习册系列答案
相关题目
要证:a2+b2-1-a2b2≤0,只要证明( )
| A、2ab-1-a2b2≤0 | ||
B、a2+b2-1-
| ||
C、
| ||
| D、(a2-1)(b2-1)≥0 |
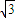 -
-
 -
-
 -
-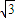
 +
+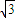
 -
-
 -
-
 -
-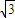
 +
+