题目内容
 (2010•潍坊三模)2010年,我国南方发生特大旱灾,为帮助灾区人民渡过灾难,我市决定组建思想觉悟高、身体素质好、抗灾技能强的青年志愿者(50周岁以下)队伍,携带资金前去支援南方某地区1000个自然村抗旱救灾.志愿者的选拔需进行测试,共准备了10组思想觉悟、身体素质与抗灾技能方面的测试项目.测试时,从备选的10组测试项目中随机抽出3组进行测试,规定:参加测试者必须完成3组测试,至少2组通过才能合格入选志愿者队伍.抗旱所携带资金与被支援自然村的海拔有关:海拔在1 000米以下(含1000米)的每村支援10万元;海拔在(1 000,2000](米)之间的每村支援20万元,…,依此类推,海拔每上升1000米,则多支援10万元(已知该地区没有海拔5000米以上的村庄),被支援村庄的海拔频率分布直方图如图.
(2010•潍坊三模)2010年,我国南方发生特大旱灾,为帮助灾区人民渡过灾难,我市决定组建思想觉悟高、身体素质好、抗灾技能强的青年志愿者(50周岁以下)队伍,携带资金前去支援南方某地区1000个自然村抗旱救灾.志愿者的选拔需进行测试,共准备了10组思想觉悟、身体素质与抗灾技能方面的测试项目.测试时,从备选的10组测试项目中随机抽出3组进行测试,规定:参加测试者必须完成3组测试,至少2组通过才能合格入选志愿者队伍.抗旱所携带资金与被支援自然村的海拔有关:海拔在1 000米以下(含1000米)的每村支援10万元;海拔在(1 000,2000](米)之间的每村支援20万元,…,依此类推,海拔每上升1000米,则多支援10万元(已知该地区没有海拔5000米以上的村庄),被支援村庄的海拔频率分布直方图如图.我市某家庭父子两人都想参加志愿者队伍,已知备选的10组测试中父亲能通过六组,儿子能通过八组.
(1)试分析我市约需准备多少支援资金;
(2)求父子至少有一人入选志愿者队伍的概率.
分析:(Ⅰ)设某村所得的支援资金为ξ万元,根据题意中的频率分布表可得ξ的分布列,由期望的计算公式,计算可得答案;
(Ⅱ)记父子通过测试为事件A、B,由组合公式可得P(A)、P(B),分析可得父子至少有一人入选志愿者队伍的对立事件为父子都没有入选志愿者队伍,即
同时发生,由相互独立事件同时发生的概率,可得P(
),由对立事件的概率性质,计算可得答案.
(Ⅱ)记父子通过测试为事件A、B,由组合公式可得P(A)、P(B),分析可得父子至少有一人入选志愿者队伍的对立事件为父子都没有入选志愿者队伍,即
. |
| A |
. |
| B |
. |
| A |
. |
| B |
解答:解:(Ⅰ)设某村所得的支援资金为ξ万元,由表可得
则Eξ=10×0.1+20×0.3+30×0.45+40×0.1+50×0.05=27(万元)
(Ⅱ)记父子通过测试为事件A、B;
P(A)=
=
=
,P(B)=
=
;
父子至少有一人入选志愿者队伍的对立事件为父子都没有入选志愿者队伍,即
同时发生,
则P(
)=(1-
)(1-
)=
,
则P(AB)=1-
=
.
| ξ | 10 | 20 | 30 | 40 | 50 |
| p | 0.1 | 0.3 | 0.45 | 0.1 | 0.05 |
(Ⅱ)记父子通过测试为事件A、B;
P(A)=
| ||||||
|
| 60+20 |
| 120 |
| 2 |
| 3 |
| ||||||
|
| 14 |
| 15 |
父子至少有一人入选志愿者队伍的对立事件为父子都没有入选志愿者队伍,即
. |
| A |
. |
| B |
则P(
. |
| A |
. |
| B |
| 2 |
| 3 |
| 14 |
| 15 |
| 1 |
| 45 |
则P(AB)=1-
| 1 |
| 45 |
| 44 |
| 45 |
点评:本题考查等可能事件的概率以及随机变量的分布列的运用与期望的计算,注意(Ⅰ)中,计算我市约需准备多少支援资金就是计算准备支援资金的期望.

练习册系列答案
相关题目
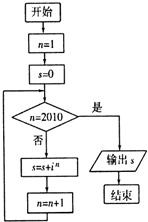 (2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )
(2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )