题目内容
已知a>0,不等式|x-4|+|x-3|<a在实数集上的解不为空集,求a的取值范围.
【答案】分析:由绝对值的几何意义知|x-4|+|x-3|表示实数轴上的点到3和到4两点的距离之和,故范围可求出,
由题意a大于|x-4|+|x-3|的最小值即可.
解答:解:由绝对值的几何意义知|x-4|+|x-3|表示实数轴上的点到3和到4两点的距离之和,
故|x-4|+|x-3|≥1,
由题意,不等式|x-4|+|x-3|<a在实数集上的解不为空集,
只要a>(|x-4|+|x-3|)min即可,
即a>1,
故答案为a>1.
点评:本题考查绝对值的几何意义,利用绝对值的几何意义求含有两个绝对值的式子的最值问题,及处理不等式的存在性求参数范围问题.
在求解过程中,注意区分存在性和恒成立.
由题意a大于|x-4|+|x-3|的最小值即可.
解答:解:由绝对值的几何意义知|x-4|+|x-3|表示实数轴上的点到3和到4两点的距离之和,
故|x-4|+|x-3|≥1,
由题意,不等式|x-4|+|x-3|<a在实数集上的解不为空集,
只要a>(|x-4|+|x-3|)min即可,
即a>1,
故答案为a>1.
点评:本题考查绝对值的几何意义,利用绝对值的几何意义求含有两个绝对值的式子的最值问题,及处理不等式的存在性求参数范围问题.
在求解过程中,注意区分存在性和恒成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
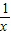 ≥2,
≥2,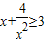 ,x+
,x+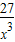 ≥4,可推广为x
≥4,可推广为x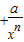 ≥
≥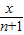 ,则a的值为( )
,则a的值为( )