Question

已知函数f(x)=-x+8x,g(x)=6lnx+m

（Ⅰ）求f(x)在区间[t,t+1]上的最大值h(t);

（Ⅱ）是否存在实数m，使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点？若存在，求出m的取值范围；，若不存在，说明理由。

Answer 1

解：（I）f(x)=－x²+8x=－(x－4)²+16,

      当t+1<4，即t<3时，f(x)在[t，t+1]上单调递增，

h(t)=f(t+1)=－(t+1)²+8(t+1)=－t²+6t+7;

当t≤4≤t+1时,即3≤t≤4时，h(t)=f(4)=16;

当t>4时，f(x)在[t，t+1]上单调递减，

h(t)=f(x)=－t²+8t .

综上，h(t)=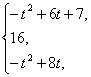     

（II）函数y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点，即函数

j(x)=g(x)－f(x)的图象与x轴的正半轴有且只有三个不同的交点。

∴j(x)=x²－8x+16ln x+m,

∵j?(x)=2x－8+            

当x∈(0,1)时，j?(x)>0，j(x)是增函数；

当x∈(1,3)时，j?(x)<0，j(x)是减函数；

当x∈(3,+∞)时，j?(x)>0，j(x)是增函数；

当x=1，或x=3时， j?(x)=0；

∴j(x)_极大值=j(1)=m－7, j(x)_极小值=j(3)=m+6ln 3－15.

∵当x充分接近0时，j(x)<0，当x充分大时，j(x)>0.

∴要使j(x)的图象与x轴正半轴有三个不同的交点，必须且只须

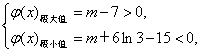    既7<m<－6ln 3.

所以存在实数m，使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点，m的取值范围为（7，15-6ln 3）.