题目内容
如图,正方体 的棱长为
的棱长为 ,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
A. | B. | C.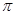 | D. |
A
解析试题分析:由题得, 圆弧 在以B为圆心,半径为BG的圆上,而圆弧
在以B为圆心,半径为BG的圆上,而圆弧 在以A为圆心,半径为AE=2的圆上.故
在以A为圆心,半径为AE=2的圆上.故 =
= ,由于
,由于 ,故
,故 ,则
,则 ,所以
,所以 +
+ =
= .故选A.
.故选A.
考点:圆弧长度的计算 球

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
四面体 中,
中, 与
与 互相垂直,
互相垂直,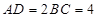 ,且
,且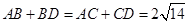 ,则四面体
,则四面体 的体积的最大值是( ) .
的体积的最大值是( ) .
| A.4 | B.2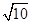 | C.5 | D. |
某三棱锥的三视图如图所示,该三棱锥的体积是( ).
A. | B. | C. | D. |
某几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
某几何体的三视图如图所示,则它的表面积为( )
A. | B. |
C. | D. |
如图所示,是某几何体的三视图,则该几何体的体积为( )
| A.9π+42 | B.36π+18 |
C. π+12 π+12 | D. π+18 π+18 |




 ),则该几何体的体积是( )
),则该几何体的体积是( )




