题目内容
在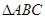 中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.
中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.
(I)若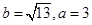 ,求边c的值;
,求边c的值;
(II)设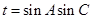 ,求
,求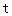 的最大值.
的最大值.
(Ⅰ)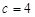 .(Ⅱ)
.(Ⅱ)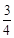 .
.
解析试题分析:(Ⅰ)由角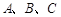 成等差数列,及
成等差数列,及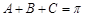 ,首先得到
,首先得到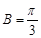 .
.
进一步应用余弦定理即得所求.
(Ⅱ)根据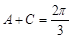 ,可化简得到
,可化简得到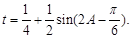
根据 ,即可得到
,即可得到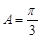 时,
时,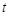 有最大值
有最大值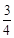 .
.
试题解析:(Ⅰ)因为角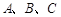 成等差数列,所以
成等差数列,所以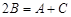 ,
,
因为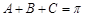 ,所以
,所以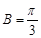 . 2分
. 2分
因为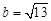 ,
,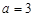 ,
,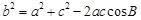 ,
,
所以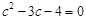 .
.
所以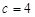 或
或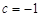 (舍去). 6分
(舍去). 6分
(Ⅱ)因为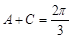 ,
,
所以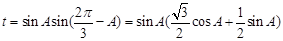
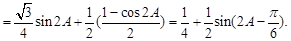 9分
9分
因为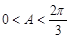 ,所以
,所以 ,
,
所以当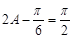 ,即
,即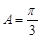 时,
时,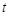 有最大值
有最大值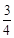 . 12分
. 12分
考点:等差数列,和差倍半的三角函数,,三角函数的性质,余弦定理的应用.

练习册系列答案
相关题目
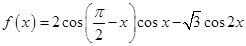 ,
,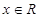 .
.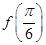 的值;
的值;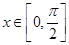 时,求
时,求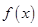 的最值.
的最值.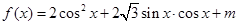 .其中
.其中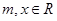
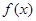 的最小正周期;
的最小正周期;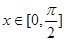 时,求实数
时,求实数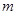 的值,使函数
的值,使函数 并求此时
并求此时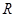 上的对称中心.
上的对称中心.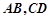 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9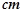 和15
和15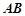 的顶部
的顶部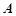 看建筑物
看建筑物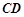 的视角
的视角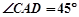 .
.
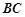 的长度;
的长度;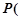 点
点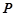 与点
与点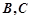 不重合),从点
不重合),从点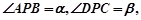 问点
问点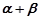 最小?
最小?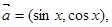
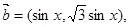
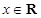 ,函数
,函数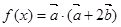 .
.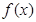 的单调递增区间;
的单调递增区间;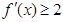 成立的
成立的 的取值集合.
的取值集合.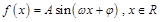 (其中
(其中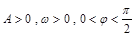 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为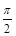 ,且图象上一个最低点为
,且图象上一个最低点为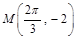 .
.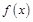 的解析式;
的解析式;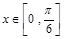 ,求
,求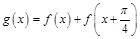 的值域.
的值域.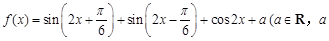 为常数).
为常数).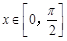 时,
时,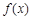 的最小值为
的最小值为 ,求a的值.
,求a的值.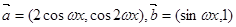 (
(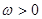 ),
),  ,且
,且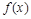 的周期为
的周期为 .
.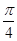 )的值;
)的值;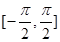 上的单调递增区间.
上的单调递增区间.