题目内容
(2010•南京三模)某校校运会期间,来自甲、乙两个班级共计6名学生志愿者随机平均分配到后勤组、保洁组、检录组,并且后勤组至少有一名甲班志愿者的概率为
(1)求6名志愿者中来自甲、乙两个班级的学生各有几人
(2)设在后勤组的甲班志愿者的人数为X,求随机变量X的概率分布列及数学期望E(X)
| 4 | 5 |
(1)求6名志愿者中来自甲、乙两个班级的学生各有几人
(2)设在后勤组的甲班志愿者的人数为X,求随机变量X的概率分布列及数学期望E(X)
分析:(1)记“至少一名甲班志愿者被分到后勤组”为事件A,则A的对立事件为“没有甲班志愿者被分到后勤组”,设甲班志愿者有x个,则1≤x<6.由P(A)=1-
=
,能求出6名志愿者中来自甲、乙两个班级的学生各有几人.(2)随机变量X的所有可能值为0,1,2.由题设条件分别求出P(X=0),P(X=1)和P(X=2)的值,由此能求出随机变量X的分布列和数学期望EX.
| ||
|
| 4 |
| 5 |
解答:解:(1)记“至少一名甲班志愿者被分到后勤组”为事件A,
则A的对立事件为“没有甲班志愿者被分到后勤组”,
设甲班志愿者有x个,则1≤x<6.
则P(A)=1-
,
∴1-
=
,
解得x=3,或x=8(舍)
答:来自甲班的志愿者有3人,来自乙班的志愿者有3人.
(2)随机变量X的所有可能值为0,1,2.
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
所以随机变量X的分布列为
数学期望EX=0×
+1×
+2×
=1.
则A的对立事件为“没有甲班志愿者被分到后勤组”,
设甲班志愿者有x个,则1≤x<6.
则P(A)=1-
| ||
|
∴1-
| ||
|
| 4 |
| 5 |
解得x=3,或x=8(舍)
答:来自甲班的志愿者有3人,来自乙班的志愿者有3人.
(2)随机变量X的所有可能值为0,1,2.
P(X=0)=
| ||
|
| 1 |
| 5 |
P(X=1)=
| ||||
|
| 3 |
| 5 |
P(X=2)=
| ||
|
| 1 |
| 5 |
所以随机变量X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
点评:本题考查概率的求法,考查离散型分布列的求法和数学期望的计算,解题时要认真审题,仔细解答,注意排列组合知识的灵活运用.

练习册系列答案
相关题目
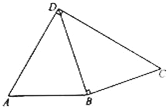 (2010•南京三模)如图,平面四边形ABCD中,∠A=60°,AD⊥CD,DB⊥BC,AB=2
(2010•南京三模)如图,平面四边形ABCD中,∠A=60°,AD⊥CD,DB⊥BC,AB=2