题目内容
10.已知数列{an}是等差数列,a1=tan225°,a5=13a1,设Sn为数列{(-1)nan}的前n项和,则S2015=( )| A. | 2015 | B. | -2015 | C. | 3024 | D. | -3022 |
分析 利用$\frac{{a}_{5}-{a}_{1}}{4}$可知公差,进而利用等差数列的性质可知S2015=-(a1+a3+…+a2015)+(a2+a4+…+a2014)=-$\frac{1}{2}$•(a1+a2015),进而计算可得结论.
解答 解:依题意,d=$\frac{{a}_{5}-{a}_{1}}{4}$=3tan225°=3,
∴an=1+3(n-1)=3n-2,
∴S2015=-(a1+a3+…+a2015)+(a2+a4+…+a2014)
=-$\frac{1008}{2}$•(a1+a2015)+$\frac{1007}{2}$(a2+a2014)
=-$\frac{1008}{2}$•(a1+a2015)+$\frac{1007}{2}$(a1+a2015)
=-$\frac{1}{2}$•(a1+a2015)
=$-\frac{1}{2}•(1+3•2015-2)$
=-3022,
故选:D.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
2.已知向量$\overrightarrow{a}$=(k,3),$\overrightarrow{b}=(1,4)$,$\overrightarrow{c}$=(1,-3),且(2$\overrightarrow{a}-3\overrightarrow{b}$)$⊥(\overrightarrow{b}+\overrightarrow{c})$,则实数k=( )
| A. | -$\frac{9}{2}$ | B. | 0 | C. | 3 | D. | $\frac{15}{2}$ |
2.已知集合A={x|x2-2x≤0},B={x|-1<x<1},则A∩B=( )
| A. | ∅ | B. | {x|-1<x≤0} | C. | {x|0≤x<1} | D. | R |
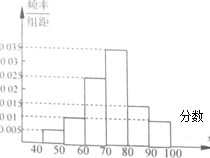 对100名学生的学习成绩进行统计,得到样本频率直方图如图所示,现规定不低于70分为合格,则合格的人数是60.
对100名学生的学习成绩进行统计,得到样本频率直方图如图所示,现规定不低于70分为合格,则合格的人数是60.