题目内容
设f（x）在点x=x0处可导，且
→1(△x→0)，则f′（xo）=（ ）
| f(xo+7△x)-f(xo) |
| △x |
| A、1 | ||
| B、0 | ||
| C、7 | ||
D、
|
分析：利用极限的运算法则求出
→
(△x→0)；利用函数在某点处的导数的定义求出f′（x0）
| f(xo+7△x)-f(xo) |
| 7△x |
| 1 |
| 7 |
解答：解：∵
→1(△x→0)
∴7•
→1(△x→0)
→
(△x→0)
∴f′(x0)=
故选D
| f(xo+7△x)-f(xo) |
| △x |
∴7•
| f(xo+7△x)-f(xo) |
| 7△x |
| f(xo+7△x)-f(xo) |
| 7△x |
| 1 |
| 7 |
∴f′(x0)=
| 1 |
| 7 |
故选D
点评：本题考查极限的运算法则、考查函数在某点处的导数的定义．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
设f（x）在点x处可导，a、b为非零常数，则
等于（ ）
| lim |
| △x→0 |
| f(x+a△x)-f(x-b△x) |
| △x |
| A、f′（x） | ||
| B、（a-b）f′（x） | ||
| C、（a+b）f′（x） | ||
D、
|
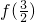的值；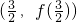
处的切线方程；
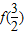的值；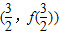
处的切线方程；
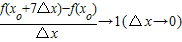，则f′（xo）=（ ）