题目内容
已知函数![]() 。(1)当
。(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;(2)当函数
处的切线方程;(2)当函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() 时,求实数
时,求实数![]() 的值;
的值;
(3)当![]() ,若函数
,若函数![]() 与
与![]() 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数![]() 的取值范围。
的取值范围。
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
(1)因为![]() ,由题意
,由题意![]() (2分)
(2分) ![]() 即过点
即过点![]() 的切线斜率为3,
的切线斜率为3,
又点![]() 则过点
则过点![]() 的切线方程为:
的切线方程为:![]() (5分)
(5分)
(2)因![]() 令
令![]() 得
得![]() 或
或![]() (1分)
(1分)
由![]() ,要使函数
,要使函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,则
,则![]()
(i)当![]() 时,当
时,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在区间[0,1]上,
在区间[0,1]上,![]()
即:![]() ,舍去 (2分)
,舍去 (2分)
(ii)当![]() 时,当
时,当![]() 时,
时,![]() ,则使函数
,则使函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
![]()
![]() 综上所述:
综上所述:![]() (2分)
(2分)
(3)设![]()
![]() 令
令![]() 得
得![]() 或
或![]() (11分)
(11分)
当![]() 时,
时,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| 1 |
|
|
| + | 0 | 一 | 0 | + |
|
|
| 极大 |
| 极小 |
|
欲使![]() 与
与![]() 图象有三个不同的交点,方程
图象有三个不同的交点,方程![]() ,也即
,也即![]()
有三个不同的实根 ,所以
,所以![]() (15分
(15分

练习册系列答案
相关题目
 .
.  时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求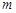 的取值范围.
的取值范围.
 。
。 时,判断
时,判断 的单调性;
的单调性; 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围; .
. 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 .
. 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围; 时,试比较
时,试比较 与
与 的大小;
的大小; (
( ).
).