题目内容
(本小题满分12分)已知函数 .
.
(Ⅰ)若函数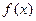 在
在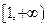 上是增函数,求正实数
上是增函数,求正实数 的取值范围;
的取值范围;
(Ⅱ)若 ,
,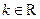 且
且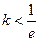 ,设
,设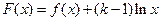 ,求函数
,求函数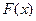 在
在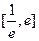 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ)解:由题设可得
因为函数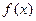 在
在 上是增函数,
上是增函数,
所以,当 时
时 ,不等式
,不等式 即
即 恒成立
恒成立
因为,当 时,
时, 的最大值为
的最大值为 ,则实数
,则实数 的取值范围是
的取值范围是 -----4分
-----4分
(Ⅱ) 解:  ,
,

所以, …………6分
…………6分
(1) 若 ,则
,则 ,在
,在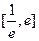 上, 恒有
上, 恒有 ,
,
所以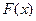 在
在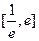 上单调递减
上单调递减 ,
, …………7分
…………7分
(2)  时
时
(i)若 ,在
,在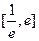 上,恒有
上,恒有
所以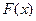 在
在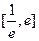 上单调递减
上单调递减
 …………9分
…………9分
ii) 时,因为
时,因为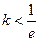 ,所以
,所以
 ,所以
,所以
所以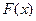 在
在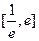 上单调递减
上单调递减
 …………11分
…………11分
综上所述:当 时,
时, ,
, ;当
;当
且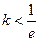 时,
时, ,
, .…………12分
.…………12分
解析

练习册系列答案
相关题目