题目内容
设命题p:函数y=lg(x2+2x-c)的定义域为R,命题q:函数y=lg(x2+2x-c)的值域为R,若命题p、q有且仅有一个正确,则c的取值范围为( )
| A.(1,+∞) | B.(-∞,-1) | C.[-1,+∞) | D.R |
∵命题p:函数y=lg(x2+2x-c)的定义域为R,
∴x2+2x-c>0的解题为R,
∴△=4+4c<0,∴c<-1.即命题p:c<-1.
∵函数y=lg(x2+2x-c)的值域为R,
∴x2+2x-c能取到所有大于零的值
这就要求抛物线t=x2+2x-c的值域包括t>0这一范围
由于其开口向上,只需判别式大于等于零
所以4-4c≥0,∴c≤1.即命题q:c≤1.
∵命题p、q有且仅有一个正确,
∴c的取值范围为c<-1.
故选B.
∴x2+2x-c>0的解题为R,
∴△=4+4c<0,∴c<-1.即命题p:c<-1.
∵函数y=lg(x2+2x-c)的值域为R,
∴x2+2x-c能取到所有大于零的值
这就要求抛物线t=x2+2x-c的值域包括t>0这一范围
由于其开口向上,只需判别式大于等于零
所以4-4c≥0,∴c≤1.即命题q:c≤1.
∵命题p、q有且仅有一个正确,
∴c的取值范围为c<-1.
故选B.

练习册系列答案
相关题目
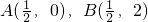 及直线
及直线 的距离相等,那么满足条件的点P有且只有1个.
的距离相等,那么满足条件的点P有且只有1个.