题目内容
7．
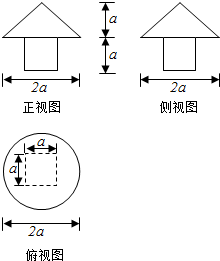一个几何体的三视图如图，则它的表面积为4a2+（1+$\sqrt{2}$）πa2，体积为a3+$\frac{1}{3}{πa}^{3}$．
分析 由已知中的三视图，可得：该几何体是一个正方体和圆锥的组合体，进而可得其表面积和体积．
解答 解：由已知中的三视图，可得：该几何体是一个正方体和圆锥的组合体，
正方体的棱长为a，故体积为：a3，
圆锥的底面直径为2a，高为a，故体积为：$\frac{1}{3}{πa}^{3}$，
故组合体的体积为：a3+$\frac{1}{3}{πa}^{3}$，
其表面积相当于圆锥的表面积与正方体的侧面积和，
正方体的侧面积为4a2，
圆锥的母线长为$\sqrt{2}a$，
故圆锥的表面积为：（1+$\sqrt{2}$）πa2，
故几何体的表面积为：4a2+（1+$\sqrt{2}$）πa2，
故答案为：4a2+（1+$\sqrt{2}$）πa2，a3+$\frac{1}{3}{πa}^{3}$
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
17．点A（sinα，cosα）在第二象限，则角α在直角坐标平面上位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
2．函数f（x）=ex+e-x，g（x）=f（2x）+mf（x），对任意x∈R，g（x）≥0，则m的取值范围是（ ）
| A． | [-4，+∞） | B． | [-1，+∞） | C． | [0，+∞） | D． | [2，+∞） |