题目内容
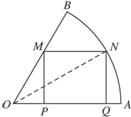
如图所示，在半径为
R的扇形OAB中，圆心角∠AOB=60°，在扇形中有一个内接矩形．求内接矩形的最大面积．
答案：略
解析：
解析：
|
解：如题图，设 PQ=x，MP=y，则矩形面积S=xy连结 ON，令∠AON=q ，则 NQ=Rsinq (0°＜q ＜60°)，对△ NOM由正弦定理有
∴  ．
故  ．
∴当 2q －60°=0，即q =30°时， ．
∴所求内接矩形的面积最大值为  ． |
练习册系列答案
相关题目
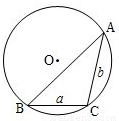
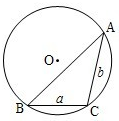通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
