题目内容
直线l过抛物线y2=2px（p＞0）的焦点，且与抛物线交于A、B两点，若线段AB的长是8，AB的中点到y轴的距离是2，则此抛物线方程是
- A.y2=12x
- B.y2=8x
- C.y2=6x
- D.y2=4x
B
分析：先设出A，B的坐标，根据抛物线的定义求得x1+x2+p=8，进而根据AB中点到y轴的距离求得p，则抛物线方程可得．
解答：设A（x1，y1），B（x2，y2），根据抛物线定义，x1+x2+p=8，
∵AB的中点到y轴的距离是2，
∴
，
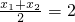∴p=4；
∴抛物线方程为y2=8x
故选B
点评：本题主要考查了抛物线的标准方程．解题的关键是利用了抛物线的定义．
分析：先设出A，B的坐标，根据抛物线的定义求得x1+x2+p=8，进而根据AB中点到y轴的距离求得p，则抛物线方程可得．
解答：设A（x1，y1），B（x2，y2），根据抛物线定义，x1+x2+p=8，
∵AB的中点到y轴的距离是2，
∴
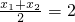，∴p=4；
∴抛物线方程为y2=8x
故选B
点评：本题主要考查了抛物线的标准方程．解题的关键是利用了抛物线的定义．
练习册系列答案
相关题目
设斜率为2的直线l过抛物线y2=ax（a≠0）的焦点F，且和y轴交于点A，若△OAF（O为坐标原点）的面积为4，则抛物线方程为（ ）
| A、y2=±4x | B、y2=4x | C、y2=±8x | D、y2=8x |
已知斜率为2的直线l过抛物线y2=ax的焦点F，且与y轴相交于点A，若△OAF（O为坐标原点）的面积为4，则抛物线方程为（ ）
| A、y2=4x | B、y2=8x | C、y2=4x或y2=-4x | D、y2=8x或y2=-8x |