题目内容
已知函数f(x)=1+
有反函数,且点M(a,b)既在函数f(x)的图象上,又在f－1(x)的图象上,求f－1(x)的表达式和点M的坐标.
解法一:由y=1+(x≥
),得2x=(y－1)2+3(y≥1),
所以f－1(x)=
(x－1)2+
(x≥1).
因为点M(a,b)在函数f(x)的图象上,
所以b=1+
. ①
又因为M(a,b)在函数f－1(x)的图象上,
所以b=
(a－1)2+
. ②
在①②中消去b,1+
=
(a－1)2+
,得
［(a－1)2－1］2［(a－1)2+2(a－1)+5］=0,
因为(a－1)2+2(a－1)+5>0恒成立,
所以(a－1)－1=0,故a=2,从而b=2.
解法二:求反函数方法同法一.
由于点M(a,b)既在函数f(x)的图象上,又在f－1(x)的图象上,则(a,b)和(b,a)都在函数f(x)的图象上,于是,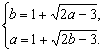
移项后两式平方相减,得(a+b－2)(a－b)=2(b－a),
即(a－b)(a+b)=0.
若a=b,易得a=b=2.
若a=－b,有b2=－4(舍去).故a=b=2.
练习册系列答案
相关题目