Question

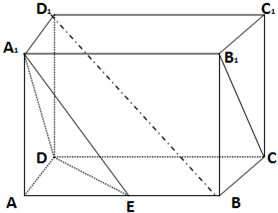如图，在长方体ABCD-A₁B₁C₁D₁中，AB=2，AD=AA₁=1，点E是棱柱AB的中点．
（1）求证：BD∥平面A₁DE；
（2）求异面直线B₁C与A₁E所成的角的大小．

Answer 1

分析：（1）取A₁B₁的中点F，通过证明平面A₁DE∥平面BFD₁，来证BD₁∥平面A₁DE．
（2）∠DA₁E为异面直线B₁C与A₁E所成的角，在△DEA₁中，求出DA₁，EA₁，DE，的长，求∠DA₁E的大小．

解答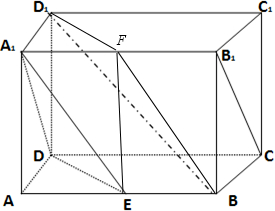：解：（1）证明：取A₁B₁的中点F，连接EF，D₁F，
∵在长方体ABCD-A₁B₁C₁D₁中，AA₁∥DD₁∥EF，EF=AA₁=DD₁，
∴四边形DEFD₁为平行四边形，∴DE∥FD₁，
又DE?平面A₁DE，FD₁?平面A₁DE，∴FD₁∥平面A₁DE，
同理可证BF∥平面A₁DE，
∵BF∩FD₁=F，∴平面A₁DE∥平面BFD₁，∵BD₁?平面BFD₁，
∴BD₁∥平面A₁DE．
（2）∵A₁D∥B₁C，∴∠DA₁E为异面直线B₁C与A₁E所成的角，
∵AD=AE=AA₁=1，
∴在△DEA₁中，DA₁=EA₁=DE=

2

，
∴∠DA₁E=

π

3

，
故异面直线B₁C与A₁E所成的角为

π

3

．

点评：本题考查了用证面面平行的方法证明线面平行，考查了求异面直线所成的角，属于中档题，解答时要注意定理的条件．