题目内容
若二面角α-l-β的一个半平面α上有一个点A，点A到棱l的距离是它到另一个平面β的距离的2倍，则这个二面角的大小为．
- A.90°
- B.60°
- C.45°
- D.30°
D
解析：
作AH⊥β交β于H，作HB⊥l于B，连结AB，由三垂线定理，HB⊥l，∴∠ABH为二面角α-l-β的平面角，由已知在Rt△ABH中，AB＝2AH，∴∠ABH＝30°．
解析：
作AH⊥β交β于H，作HB⊥l于B，连结AB，由三垂线定理，HB⊥l，∴∠ABH为二面角α-l-β的平面角，由已知在Rt△ABH中，AB＝2AH，∴∠ABH＝30°．
练习册系列答案
字词句段篇系列答案
相关题目
若二面角α-l-β的大小为
，直线m⊥α，则β所在平面内的直线与m所成角的取值范围是（ ）
| π |
| 3 |
A、(0，
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
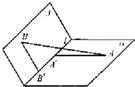如图，α和β为平面，α∩β=l，A∈α，B∈β，AB=5，A，B在棱l上的射影分别为A′，B′，AA′=3，BB′=2．若二面角α-l-β的大小为