题目内容
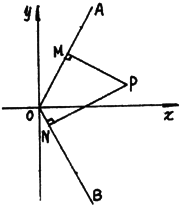
已知:如图,射线OA为y=2x(x>0),射线OB为y= –2x(x>0),动点P(x, y)在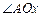 的内部,
的内部,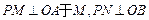 于N,四边形ONPM的面积为2..
于N,四边形ONPM的面积为2..
(I)动点P的纵坐标y是其横坐标x的函数,求这个函数y=f(x)的解析式;
(II)确定y=f(x)的定义域.
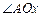 的内部,
的内部,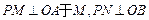 于N,四边形ONPM的面积为2..
于N,四边形ONPM的面积为2..(I)动点P的纵坐标y是其横坐标x的函数,求这个函数y=f(x)的解析式;
(II)确定y=f(x)的定义域.
 |
(1) (2)
(2)
 (2)
(2)
(Ⅰ)设 ,
,
 .
.
则 ,
,
由动点 在
在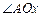 的内部,得
的内部,得 .
.
∴ ,
,
∴

∴ ①
①
又 ,
,
分别解得 ,
,
代入①式消去 、
、 ,并化简得
,并化简得 .
.
∵ ,∴
,∴ .
.
(Ⅱ)由 在
在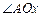 内部,得
内部,得 .
.
又垂足 必须在射线
必须在射线 上,否则
上,否则 、
、 、
、 、
、 四点不能构成四边形,所以还必须满足条件
四点不能构成四边形,所以还必须满足条件
∴


所以 的定义域为
的定义域为
 ,
,
 .
.则
 ,
,
由动点
 在
在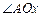 的内部,得
的内部,得 .
.∴
 ,
,
∴


∴
 ①
①又
 ,
,
分别解得
 ,
,
代入①式消去
 、
、 ,并化简得
,并化简得 .
.∵
 ,∴
,∴ .
.(Ⅱ)由
 在
在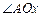 内部,得
内部,得 .
.又垂足
 必须在射线
必须在射线 上,否则
上,否则 、
、 、
、 、
、 四点不能构成四边形,所以还必须满足条件
四点不能构成四边形,所以还必须满足条件
∴



所以
 的定义域为
的定义域为

练习册系列答案
相关题目
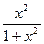

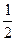 ),f(3)与f(
),f(3)与f(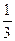 );
);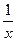 )有什么关系?并证明你的结论;
)有什么关系?并证明你的结论;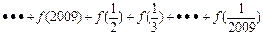 的值.
的值.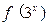 =
=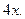
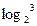 +233,求
+233,求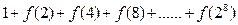 的值
的值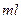 到110
到110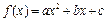 ,其中
,其中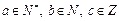 .
.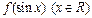 的最大值为2,最小值为-4,试求函数f(x)的最小值;
的最大值为2,最小值为-4,试求函数f(x)的最小值;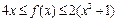 恒成立,且存在
恒成立,且存在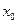 使得
使得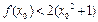 成立,求c的值.
成立,求c的值.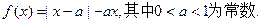
 ,则a的取值范围是 ( )
,则a的取值范围是 ( )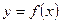 是最小正周期为2的函数,当
是最小正周期为2的函数,当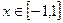 时,
时,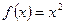 ,则函数
,则函数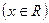 图像与
图像与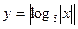 图像的交点的个数是( )
图像的交点的个数是( )