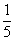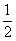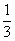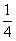题目内容
ABCD为长方形，AB＝2，BC＝1，O为AB的中点，在长方形ABCD内随机取一点，取到的点到O的距离大于1的概率为：
A． | B． | C． | D． |
A
解析试题分析：本题利用几何概型解决，这里的区域平面图形的面积．欲求取到的点到O的距离大于1的概率，只须求出圆外的面积与矩形的面积之比即可．解：
根据几何概型得：取到的点到O的距离大于1的概率：P=圆外部分的面积: 矩形的面积=
,故答案为A.
考点：几何概型
点评：本题主要考查几何概型．如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
如果随机变量§~N（—2，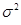
），且P（—3≤§≤—1）=0.4，则P（§≥—1）=
| A．0.7 | B．0.6 | C．0.3 | D．0.2 |
设随机变量
服从正态分布
.若
，则
的值为（ ）
A． | B． | C． | D． |
下图的程序框图中
是产生随机数的函数,它能随机产生区间
内的任何一个数,如果输入N值为4000,输出的m值为1840,则利用随机模拟方法计算由
与
及
轴所围成面积的近似值为( )
| A．0.46 | B．2.16 | C．1.84 | D．0.54 |
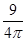
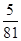
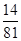
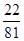
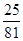
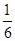B. 
C. 
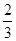D. 
