题目内容
已知数列{an}和{bn}满足:a1=λ,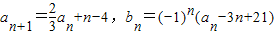 ,其中λ为实数,n为正整数.
,其中λ为实数,n为正整数.(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由.
【答案】分析:(1)这种证明数列不是等比数列的问题实际上不好表述,我们可以选择反证法来证明,假设存在推出矛盾.
(2)用数列an构造一个新数列,我们写出新数列的第n+1项和第n项之间的关系,发现λ的取值影响数列的性质,所以要对λ进行讨论.
(3)根据前面的运算写出数列的前n项和,把不等式写出来观察不等式的特点,构造新函数,根据函数的最值进行验证,注意n的奇偶情况要分类讨论.
解答:解:(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即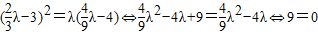 ,矛盾.
,矛盾.
所以{an}不是等比数列.
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n+1)+21]=(-1)n+1( an-2n+14)
an-2n+14)
= (-1)n•(an-3n+21)=-
(-1)n•(an-3n+21)=- bn
bn
又b1=-(λ+18),所以
当λ=-18,bn=0(n∈N+),此时{bn}不是等比数列:
当λ≠-18时,b1=(λ+18)≠0,由上可知bn≠0,
∴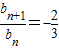 (n∈N+).
(n∈N+).
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,- 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn=-(λ+18)•(- )n-1,于是可得
)n-1,于是可得
Sn=-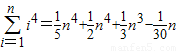 ,
,
要使a<Sn<b对任意正整数n成立,
即a<- (λ+18)•[1-(-
(λ+18)•[1-(- )n]<b(n∈N+)
)n]<b(n∈N+)
得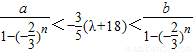
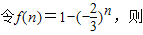 ①
①
当n为正奇数时,1<f(n)≤ ;当n为正偶数时,
;当n为正偶数时,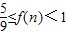 ,
,
∴f(n)的最大值为f(1)= ,f(n)的最小值为f(2)=
,f(n)的最小值为f(2)= ,.
,.
于是,由①式得 a<-
a<- (λ+18)<
(λ+18)<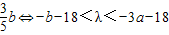 .
.
当a<b≤3a时,由-b-18≥=-3a-18,不存在实数满足题目要求;
当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<b,且λ的取值范围是(-b-18,-3a-18)
点评:这道题目的难度要高于高考题的难度,若函数题是一套卷的压轴题,可以出到这个难度,否则本题偏难,本小题主要考查等比数列的定义、数列求和、不等式等基础知识和分类讨论的思想,考查综合分析问题的能力和推理认证能力.
(2)用数列an构造一个新数列,我们写出新数列的第n+1项和第n项之间的关系,发现λ的取值影响数列的性质,所以要对λ进行讨论.
(3)根据前面的运算写出数列的前n项和,把不等式写出来观察不等式的特点,构造新函数,根据函数的最值进行验证,注意n的奇偶情况要分类讨论.
解答:解:(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即
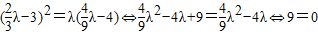 ,矛盾.
,矛盾.所以{an}不是等比数列.
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n+1)+21]=(-1)n+1(
 an-2n+14)
an-2n+14)=
 (-1)n•(an-3n+21)=-
(-1)n•(an-3n+21)=- bn
bn又b1=-(λ+18),所以
当λ=-18,bn=0(n∈N+),此时{bn}不是等比数列:
当λ≠-18时,b1=(λ+18)≠0,由上可知bn≠0,
∴
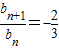 (n∈N+).
(n∈N+).故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
 为公比的等比数列.
为公比的等比数列.(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn=-(λ+18)•(-
 )n-1,于是可得
)n-1,于是可得Sn=-
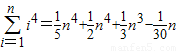 ,
,要使a<Sn<b对任意正整数n成立,
即a<-
 (λ+18)•[1-(-
(λ+18)•[1-(- )n]<b(n∈N+)
)n]<b(n∈N+)得
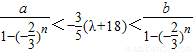
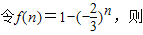 ①
①当n为正奇数时,1<f(n)≤
 ;当n为正偶数时,
;当n为正偶数时,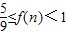 ,
,∴f(n)的最大值为f(1)=
 ,f(n)的最小值为f(2)=
,f(n)的最小值为f(2)= ,.
,.于是,由①式得
 a<-
a<- (λ+18)<
(λ+18)<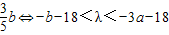 .
.当a<b≤3a时,由-b-18≥=-3a-18,不存在实数满足题目要求;
当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<b,且λ的取值范围是(-b-18,-3a-18)
点评:这道题目的难度要高于高考题的难度,若函数题是一套卷的压轴题,可以出到这个难度,否则本题偏难,本小题主要考查等比数列的定义、数列求和、不等式等基础知识和分类讨论的思想,考查综合分析问题的能力和推理认证能力.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目