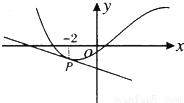
题目内容
 如图,函数g(x)=xf(x)+x3-1的图象在点P处的切线方程是y=-
如图,函数g(x)=xf(x)+x3-1的图象在点P处的切线方程是y=-| 1 | 2 |
分析:求出g(x)的导函数,由函数图象可知切点P的横坐标为-2,把x=-2代入导函数中得到一个关系式,记作(*),又把x=-2代入切线方程求出切点的纵坐标,确定出切点坐标,把求出的切点坐标代入g(x)中,即可求出f(-2)的值,然后把求出的f(-2)的值代入(*)中即可求出f′(-2)的值,进而求出f(-2)+f′(-2)的值.
解答:解:求导得:g′(x)=f(x)+xf′(x)+3x2,
把x=-2代入得:g′(-2)=f(-2)-2f′(-2)+12=-
(*),
把x=-2代入切线方程得:y=-1,
所以切点坐标为(-2,-1),即g(-2)=-2f(-2)-9=-1,
解得:f(-2)=-4,
把f(-2)=-4代入(*)得:-4-2f′(-2)+12=-
,
解得:f′(-2)=
,
则f(-2)+f′(-2)=-4+
=
.
故答案为:
把x=-2代入得:g′(-2)=f(-2)-2f′(-2)+12=-
| 1 |
| 2 |
把x=-2代入切线方程得:y=-1,
所以切点坐标为(-2,-1),即g(-2)=-2f(-2)-9=-1,
解得:f(-2)=-4,
把f(-2)=-4代入(*)得:-4-2f′(-2)+12=-
| 1 |
| 2 |
解得:f′(-2)=
| 17 |
| 4 |
则f(-2)+f′(-2)=-4+
| 17 |
| 4 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:根据函数图象得到切点P的横坐标是本题的突破点,解此类题的思路是采用数形结合的思想.同时要求学生掌握求导法则及直线与曲线交点的特点,会利用导数求曲线上过某点切线方程的斜率.

练习册系列答案
相关题目
 设函数f(x)=sinx,g(x)=
设函数f(x)=sinx,g(x)=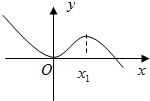 如图,函数f(x)=ax3+bx2+cx+d图象与x轴相切于原点.
如图,函数f(x)=ax3+bx2+cx+d图象与x轴相切于原点.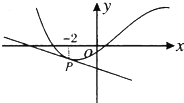 如图,函数g(x)=xf(x)+x3-1的图象在点P处的切线方程是
如图,函数g(x)=xf(x)+x3-1的图象在点P处的切线方程是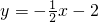 ,且f(x)也是可导函数,则f(-2)+f(-2)等于________.
,且f(x)也是可导函数,则f(-2)+f(-2)等于________. ,且f(x)也是可导函数,则f(-2)+f(-2)等于 .
,且f(x)也是可导函数,则f(-2)+f(-2)等于 .