题目内容
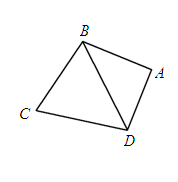
(本小题满分14分)如图,有三个生活小区(均可看成点)分别位于 三点处,
三点处, ,
, 到线段
到线段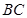 的距离
的距离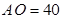 ,
,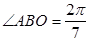 (参考数据:
(参考数据: 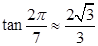 ). 今计划建一个生活垃圾中转站
). 今计划建一个生活垃圾中转站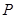 ,为方便运输,
,为方便运输,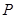 准备建在线段
准备建在线段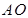 (不含端点)上.
(不含端点)上.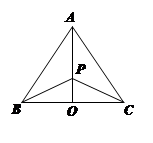
(1)设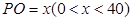 ,试将
,试将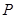 到三个小区距离的最远者
到三个小区距离的最远者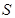 表示为
表示为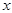 的函数,并求
的函数,并求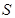 的最小值;
的最小值;
(2)设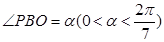 ,试将
,试将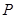 到三个小区的距离之和
到三个小区的距离之和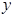 表示为
表示为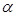 的函数,并确定当
的函数,并确定当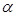 取何值时,可使
取何值时,可使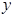 最小?
最小?
(1)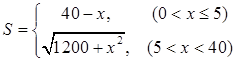 当
当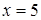 时,
时,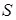 取得小值为35
取得小值为35
(2)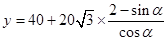 ,当
,当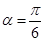 时,
时,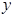 最小
最小
解析试题分析:(1)在 中,因为
中,因为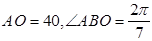 ,所以
,所以 ,
,
所以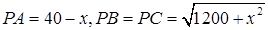 ………………………………2分
………………………………2分
①若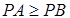 ,即
,即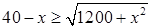 ,即
,即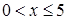 时,
时, 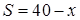 ;
;
②若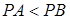 ,即
,即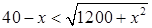 ,即
,即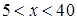 时,
时, 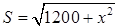 .
.
从而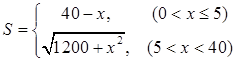 …………………………………………4分
…………………………………………4分
当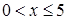 时,
时,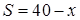 在
在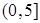 上是减函数,∴
上是减函数,∴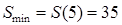 ;
;
当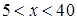 时,
时,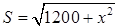 在
在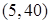 上是增函数,∴
上是增函数,∴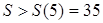 ,
,
综上所述,当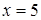 时,
时,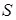 取得小值为35………………………………………7分
取得小值为35………………………………………7分
(2)在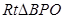 中,
中, 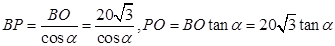 ……………………9分
……………………9分
又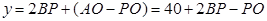 ,
,
所以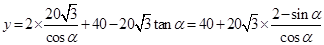 ………………………11分
………………………11分
因为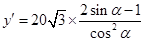 ,令
,令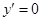 ,即
,即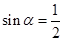 ,从而
,从而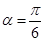 ,
,
当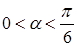 时,
时,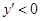 ;当
;当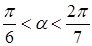 时,
时, 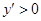 .
.
∴当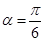 时,可使
时,可使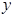 最小……………………………………14分
最小……………………………………14分
考点:分段函数,利用导数求函数最值
点评:本题难度较大,第二问中求y最值不易想到导数工具

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
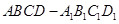 的底面边长为2,
的底面边长为2, .
.
 为线段
为线段 的中点,求
的中点,求 与平面
与平面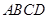 所成角的大小.
所成角的大小. ,BC=CD=BD,设
,BC=CD=BD,设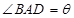 .
.
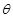 的函数;
的函数; 中,
中, ,将
,将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
. 的表面积和体积.
的表面积和体积.
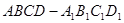 中,
中, ,
,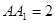 ,
,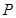 为
为 的中点。
的中点。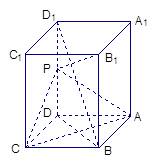
 ∥平面
∥平面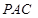 ;
; 平面
平面 ;
;
 的底面为直角梯形,
的底面为直角梯形,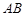 //
//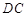 ,
,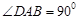 ,
,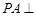 底面
底面 ,且
,且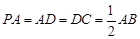 .
.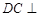 平面
平面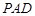 ;
; 的余弦值的大小.
的余弦值的大小.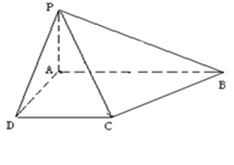
 时,有DN ∥平面AEM,求
时,有DN ∥平面AEM,求  的值;
的值;
 中,
中, ,
, ,点
,点 在棱
在棱 上移动.
上移动.
 //平面
//平面 ;
; ⊥
⊥ ;
; 的体积.
的体积.