题目内容
设函数f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线与直线x﹣6y﹣7=0垂直,导函数f'(x)的最小值为﹣12.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调递增区间,并求函数f(x)在[﹣1,3]上的最大值和最小值.
考点:
利用导数研究函数的单调性;函数奇偶性的性质;利用导数研究函数的极值;两条直线垂直的判定.
专题:
综合题.
分析:
(Ⅰ)先根据奇函数求出c的值,再根据导函数f'(x)的最小值求出b的值,最后依据在x=1处的导数等于切线的斜率求出c的值即可;
(Ⅱ)先求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求得区间即为单调区间,根据极值与最值的求解方法,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,最小的一个就是最小值.
解答:
解:(Ⅰ)∵f(x)为奇函数,
∴f(﹣x)=﹣f(x)
即﹣ax3﹣bx+c=﹣ax3﹣bx﹣c
∴c=0
∵f'(x)=3ax2+b的最小值为﹣12
∴b=﹣12
又直线x﹣6y﹣7=0的斜率为![]()
因此,f'(1)=3a+b=﹣6
∴a=2,b=﹣12,c=0.
(Ⅱ)f(x)=2x3﹣12x.![]() ,列表如下:
,列表如下:
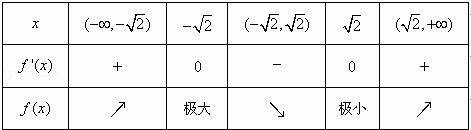
所以函数f(x)的单调增区间是![]() 和
和![]()
∵f(﹣1)=10,![]() ,f(3)=18
,f(3)=18
∴f(x)在[﹣1,3]上的最大值是f(3)=18,最小值是![]() .
.
点评:
本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |