题目内容
若函数 的图象在x=0处的切线l与圆C:x2+y2=1相离,则点P(a,b)与圆C的位置关系是 .
的图象在x=0处的切线l与圆C:x2+y2=1相离,则点P(a,b)与圆C的位置关系是 .
【答案】分析:根据题意利用导数求出切线的斜率以及切点,进而求出切线方程,结合切线l与圆C:x2+y2=1相离,得到 即可得到答案.
即可得到答案.
解答:解:由题意可得:函数 ,所以
,所以 ,
,
所以切线的斜率为 .
.
根据题意可得切点为(0, ),
),
所以切线的方程为: .
.
所以圆心(0,0)到直线 的距离为:d=
的距离为:d= .
.
因为切线l与圆C:x2+y2=1相离,
所以 ,即
,即 ,
,
所以点P(a,b)与圆C的位置关系是点P在圆内.
故答案为:点P在圆内.
点评:本题主要考查导数的几何意义以及直线、点与圆的位置关系,并且加以正确的运算.
 即可得到答案.
即可得到答案.解答:解:由题意可得:函数
 ,所以
,所以 ,
,所以切线的斜率为
 .
.根据题意可得切点为(0,
 ),
),所以切线的方程为:
 .
.所以圆心(0,0)到直线
 的距离为:d=
的距离为:d= .
.因为切线l与圆C:x2+y2=1相离,
所以
 ,即
,即 ,
,所以点P(a,b)与圆C的位置关系是点P在圆内.
故答案为:点P在圆内.
点评:本题主要考查导数的几何意义以及直线、点与圆的位置关系,并且加以正确的运算.

练习册系列答案
相关题目
 的图象在x=0处的切线
的图象在x=0处的切线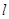 与圆
与圆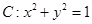 相离,则
相离,则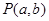 与圆C的位置关系是( )
与圆C的位置关系是( )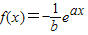 的图象在x=0处的切线l与圆C:x2+y2=1相离,则点P(a,b)与圆C的位置关系是 .
的图象在x=0处的切线l与圆C:x2+y2=1相离,则点P(a,b)与圆C的位置关系是 .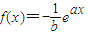 的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )
的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )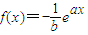 的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )
的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )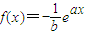 的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )
的图象在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )