设F1.F2为椭圆的两个焦点,P为椭圆上一点,已知P.F1.F2是一个直角三角形的三个顶点,且|PF1|＞|PF2|,求的值. 题目和参考答案——青夏教育精英家教网—

题目内容

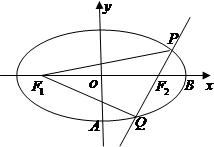
设F₁、F₂为椭圆的两个焦点,P为椭圆上一点,已知P、F₁、F₂是一个直角三角形的三个顶点,且|PF₁|＞|PF₂|,求的值.

解:由题可得|PF₁|+|PF₂|=6,|F₁F₂|=2.

若∠PF₂F₁为直角,则|PF₁|²=|PF₂|²+|F₁F₂|²,

即|PF₁|²=(6-|PF₁|)²+20,

∴,.∴.

若∠F₁PF₂为直角,则|F₁F₂|²=|PF₁|²+|PF₂|²,

即20=|PF₁|²+(6-|PF₁|)²,

得|PF₁|=4,|PF₂|=2,∴.

启示:涉及椭圆的焦点和椭圆上一点之间的距离问题,常利用椭圆的定义来解决.

练习册系列答案

相关题目

=1的中心任作一直线与椭圆交于PQ两点，当四边形PF₁QF₂面积最大时，

．

，过点A（0，-b）和B（a，0）的直线与原点的距离为

．
（1）求椭圆的方程；
（2）设F₁、F₂为椭圆的左、右焦点，过F₂作直线交椭圆于P、Q两点，求△PQF₁的内切圆半径r的最大值．

设F₁，F₂为椭圆的两个焦点，若椭圆上存在点P满足∠F₁PF₂=120°，则椭圆的离心率的取值范围是（　　）

设F₁，F₂为椭圆的两个焦点，|F₁F₂|=8，P为椭圆上的一点，|PF₁|+|PF₂|=10，PF₁⊥PF₂，则点P的个数是（　　）

（2006•蓟县一模）设F₁、F₂为椭圆的两个焦点，A为椭圆上的点，且

试题分类