题目内容
如图所示，设k1，k2，k3分别是直线l1，l2，l3的斜率，则（ ）分析：由于直线l1的倾斜角为锐角，可得k1＞0．由于直线l2和 l3的倾斜角都是钝角，且直线l2的倾斜角大于 l3的倾斜角，故有 0＞k2＞k3．
解答：解：由于只有直线l1的倾斜角为锐角，故只有直线l1的斜率为正数，即k1＞0．
由于直线l2和 l3的倾斜角都是钝角，且直线l2的倾斜角大于 l3的倾斜角，故有直线l2的斜率大于 l3的斜率，故有 0＞k2＞k3．
综上可得 k3＜k2＜k1，
故选C．
由于直线l2和 l3的倾斜角都是钝角，且直线l2的倾斜角大于 l3的倾斜角，故有直线l2的斜率大于 l3的斜率，故有 0＞k2＞k3．
综上可得 k3＜k2＜k1，
故选C．
点评：本题主要考查直线的倾斜角和斜率的关系，由直线的图象特征判断它们的斜率间的关系，属于基础题．
练习册系列答案
相关题目
函数f（x）=2x和g（x）=x3的图象的示意图如图所示，设两函数的图象交于点 A（x1，y1），B（x2，y2），且x1＜x2．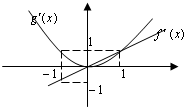
（2011•乐山一模）已知函数f′（x）、g′（x）分别是二次函数f（x）和三次函数g（x）的导函数，它们在同一坐标系下的图象如图所示，设函数h（x）=f（x）-g（x），则h（-1），h（0），h（1）的大小关系为
