题目内容

若A、B与 F1、F2分别为椭圆C：
x2
5
+y2=1的两长轴端点与两焦点，椭圆C上的点P使得∠F1PF2=
π
2
，则tan∠APB=
-
5
-
5
．
分析：由椭圆的定义和勾股定理，算出点P在第一象限时的坐标为P（
15
2
，
1
2
），再由直线PA、PB的倾斜角与∠APB的关系，结合斜率公式和正切的差角公式，即可算出tan∠APB的值．
解答：解：根据题意，∠APB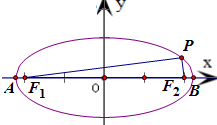的大小与点P在哪一象限无关，因此以点P在第一象限为例，设P（m，n）
∵|PF1|+|PF2|=2a=2
5
，|PF1|2+|PF2|2=4c2=16
∴|PF1|•|PF2|=
1
2
[（|PF1|+|PF2|）2-（|PF1|2+|PF2|2）]=2
由此可得，△PF1F2的面积S=
1
2
|PF1|•|PF2|=1
又∵△PF1F2的面积S=
1
2
|F1F2|•n=1
∴n=
2
2c
=
1
2
，代入椭圆方程可得m=
15
2
，得P（
15
2
，
1
2
）
因此：kPA=
1
2
-0
15
2
+
5
=
1
15
+2
5
，kPB=
1
2
-0
15
2
-
5
=
1
15
-2
5

∵∠APB等于PB的倾斜角减去PA的倾斜角
∴tan∠APB=
kPB-kPA
1+k PBkPA
=
1
15-2
5
-
1
15
+2
5
1+
1
15
-2
5
×
1
15
+2
5
=-
5

故答案为：
5
点评：本题给出椭圆上一点对两个焦点所张的角为直角，求该点与长轴两个顶点所张角的正切值，着重考查了直线的斜率公式、两角差的正切公式和椭圆的几何性质等知识，属于中档题．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，过右焦点F且倾斜角为
π
3
的直线与C相交于A、B两点，且3
AF
=5
FB
．
（1）求椭圆的离心率；
（2）若△ABF1的面积小于等于
8
3
5
（F1为左焦点），求弦AB长度的取值范围．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
2
2
．
（1）若圆（x-2）2+（y-1）2=
20
3
与椭圆相交于A、B两点且线段AB恰为圆的直径，求椭圆的方程；
（2）设L为过椭圆右焦点F的直线，交椭圆于M、N两点，且L的倾斜角为60°．求
|MF|
|NF|
的值．
（3）在（1）的条件下，椭圆W的左右焦点分别为F1、F2，点R在直线l：x-
3
y+8=0上．当∠F1RF2取最大值时，求
|RF1|
|RF2|
的值．
已知△OFQ的面积为2
6
，且
OF
•
FQ
=m．
（1）设
6
＜m＜4
6
，求向量
OF
与
FQ
的夹角θ正切值的取值范围；
（2）设以O为中心，F为焦点的双曲线经过点Q（如图），|
OF
|=c，m=(
6
4
-1)c2，当|
OQ
|取得最小值时，求此双曲线的方程．
（3）设F1为（2）中所求双曲线的左焦点，若A、B分别为此双曲线渐近线l1、l2上的动点，且2|AB|=5|F1F|，求线段AB的中点M的轨迹方程，并说明轨迹是什么曲线．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
2
2
，左、右焦点分别为
F1，F2，点P（2，
3
），点F2在线段PF1的中垂线上．
（1）求椭圆C的方程；
（2）设直线l1：y=kx+m与椭圆C交于M、N两点，直线F2M与F2N的倾斜角分别为α，β，且α+β=π，求证：直线l1经过定点，并求该定点的坐标．
（3）若过点B（2，0）的直线l2（斜率不等于零）与椭圆C交于不同的两点E，F（E在B，F之间），△OBE与△OBF的面积之比为
1
2
，求直线l2的方程．
下列说法中，正确的有
 
．
①若点P（x0，y0）是抛物线y2=2px上一点，则该点到抛物线的焦点的距离是|PF|=x0+
p
2
；
②设F1、F2为双曲线
x2
a2
-
y2
b2
=1的两个焦点，P（x0，y0）为双曲线上一动点，∠F1PF2=θ，则△PF1F2的面积为b2tan
θ
2
；
③设定圆O上有一动点A，圆O内一定点M，AM的垂直平分线与半径OA的交点为点P，则P的轨迹为一椭圆；
④设抛物线焦点到准线的距离为p，过抛物线焦点F的直线交抛物线于A、B两点，则
1
|AF|
、
1
p
、
1
|BF|
成等差数列．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网