题目内容
已知命题A：函数f(x)=x2-4mx+4m2+2在区间[-1，4]上的最小值为2；命题B：{x|m≤x≤2m+1(m≥-1)}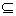
{x|x2-4≥0}，若A、B至少有一个为真命题，试求实数m的取值范围。
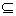{x|x2-4≥0}，若A、B至少有一个为真命题，试求实数m的取值范围。 解：∵f(x)=x2-4mx+4m2+2=(x-2m)2+2，
∴只有x=2m时，f(x)的最小值为2，
又∵f(x)在区间[-1，4]上的最小值为2，
∴-1≤2m≤4，
∴
≤m≤2，即命题A为真的条件是≤m≤2；
∵{x|m≤x≤2m+1（m≥-1）}
{x|x2-4≥0}，
∴
或
，
∴m≥2或m
，即命题B为真的条件是m≥2；
∵命题A、B至少有一个为真命题，
由A∪B={x|x≥
}，
得命题A、B至少有一个为真命题的条件是m≥，
∴m的取值范围是[
，+∞)。
∴只有x=2m时，f(x)的最小值为2，
又∵f(x)在区间[-1，4]上的最小值为2，
∴-1≤2m≤4，
∴
≤m≤2，即命题A为真的条件是≤m≤2； ∵{x|m≤x≤2m+1（m≥-1）}
{x|x2-4≥0}，∴
或，∴m≥2或m
，即命题B为真的条件是m≥2；∵命题A、B至少有一个为真命题，
由A∪B={x|x≥
}， 得命题A、B至少有一个为真命题的条件是m≥
，∴m的取值范围是[
，+∞)。
练习册系列答案
相关题目
已知命题p：函数f（x）=log0.5（2-x）定义域为（-∞，2）；命题q：若k＜0则函数g(x)=
在（0，+∞）上是减函数，对以上两个命题，下列结论正确的是（ ）
| k |
| x |
| A、命题“p且q”为真 |
| B、命题“p或 q”为假 |
| C、命题“P或﹁p”为假 |
| D、命题“﹁p且﹁q”为假 |