Question

（2012•上高县模拟）点M（x，y）是不等式组

0≤x≤2 y≤3 x≤3y

表示的平面区域Ω内的一动点，使y-2x的值取得最小的点为A（x₀，y₀），则

OM

•

OA

（O为坐标原点）的取值范围是

[0，6]

．

Answer 1

分析：画出满足约束条件

0≤x≤2 y≤3 x≤3y

的平面区域Ω，然后利用角点法求出满足条件使Z=y-2x的值取得最小的点A的坐标，结合平面向量的数量积运算公式，即可得到结论．

解答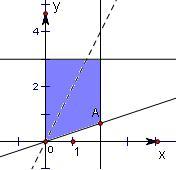：解：满足约束条件

0≤x≤2 y≤3 x≤3y

的平面区域Ω如下图所示：
由图可知，当x=2，y=

2

3

时，Z=y-2x取得最小值．
故

OA

=（2，

2

3

），

OM

=（x，y）
则

OM

•

OA

=2x+

2

3

y，
则当M与O重合时，

OM

•

OA

取最小值0；
当M点坐标为（2，3）时，

OM

•

OA

取最大值6，
故则

OM

•

OA

（O为坐标原点）的取值范围是[0，6]
故答案为：[0，6]．

点评：本题考查的知识点是简单线性规划，及平面向量的数量积的运算，其中根据约束条件画出可行域，进而根据角点法求出最优解是解答本题的关键．