题目内容
15.在直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,求证:A1C⊥BC1.
分析 连接AC1,根据AA1=AC可得到A1C⊥AC1,而根据线面垂直的判定定理AB⊥平面ACC1A1,从而得到A1C⊥AB,所以根据线面垂直的判定定理可得到A1C⊥平面ABC1,所以A1C⊥BC1.
解答 证明:如图,连接AC1;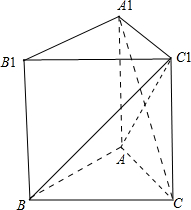 AA1=AC;
AA1=AC;
∴四边形ACC1A1是菱形;
∴A1C⊥AC1;
AA1⊥底面ABC,AB?底面ABC;
∴AA1⊥AB,即AB⊥AA1;
又AB⊥AC;C1A1
∴AB⊥平面ACC1A1,A1C?平面ACC1A1
∴AB⊥A1C,即A1C⊥AB,AB∩AC1=A;
∴A1C⊥平面ABC1,BC1?平面ABC1;
∴A1C⊥BC1.
点评 考查要证明线线垂直可转化为证明线面垂直,以及菱形的定义,菱形对角线的特点,直棱柱的侧棱和底面的关系,线面垂直的判定定理.

练习册系列答案
相关题目
10.抛物线x2-2y-6xsinθ-9cos2θ+8cosθ+9=0的顶点的轨迹是(其中θ∈R)( )
| A. | 圆 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
5.若点(sinα,sin2α)位于第四象限,则角α在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 客车和货车两车同时从A站出发向两个不同方向行驶,5小时后再C站相遇(如图所示,四边形是长方形)已知B、C两站相距20千米,货车速度比客车速度慢$\frac{1}{4}$,客车每小时行驶多少千米?货车呢?
客车和货车两车同时从A站出发向两个不同方向行驶,5小时后再C站相遇(如图所示,四边形是长方形)已知B、C两站相距20千米,货车速度比客车速度慢$\frac{1}{4}$,客车每小时行驶多少千米?货车呢?