题目内容
如图,正四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,底面边长为2
中,底面边长为2![]() ,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D
,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D![]() 到平面B
到平面B![]() EF的距离d。
EF的距离d。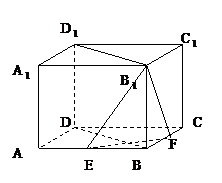
点D![]() 到平面EFB
到平面EFB![]() 的距离为
的距离为![]()
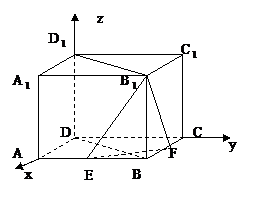
解析:
如图,建立空间直角坐标系D-xyz。易得D![]() (0,0,4),B
(0,0,4),B![]() (2
(2![]() ,2
,2![]() ,4),
,4),
E(2![]() ,
,![]() ,0),F(
,0),F(![]() ,2
,2![]() ,0),
,0),
故![]() =(-
=(-![]() ,
,![]() ,0),
,0),![]() =(0,
=(0,![]() ,4),
,4),![]() =(2
=(2![]() ,2
,2![]() ,0),
,0),
设![]() =(x,y,z)是平面B
=(x,y,z)是平面B![]() EF的法向量,
EF的法向量,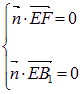
![]()
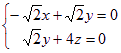 ,令x=1,得
,令x=1,得![]() =(1,1,-
=(1,1,-![]() )。则|
)。则|![]() ·
·![]() |=4
|=4![]() ,∴d=
,∴d=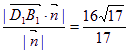 。
。
故点D![]() 到平面EFB
到平面EFB![]() 的距离为
的距离为![]() 。
。

练习册系列答案
相关题目
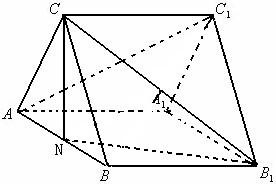 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
