题目内容
已知函数f(x)=sinx+cosx,f′(x)是f(x)的导函数。
(1)求函数F(x)=f(x)f′(x)+f2(x)的值域和最小正周期;
(2)若f(x)=2f′(x),求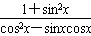 的值。
的值。
(1)求函数F(x)=f(x)f′(x)+f2(x)的值域和最小正周期;
(2)若f(x)=2f′(x),求
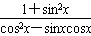 的值。
的值。解:(1)∵f′(x)=cosx-sinx,
∴F(x)=f(x)f′(x)+f2(x)
=cos2x-sin2x+1+2sinxcosx
=1+sin2x+cos2x
=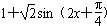
函数F(x)的值域为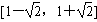
最小正周期为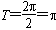 。
。
(2)∵f(x)=2f′(x)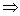 sinx+cosx=2cosx-2sinx,
sinx+cosx=2cosx-2sinx,
∴cosx=3sinx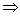 tanx=
tanx=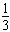
∴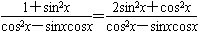
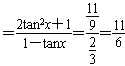 。
。
∴F(x)=f(x)f′(x)+f2(x)
=cos2x-sin2x+1+2sinxcosx
=1+sin2x+cos2x
=
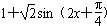
函数F(x)的值域为
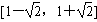
最小正周期为
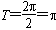 。
。(2)∵f(x)=2f′(x)
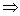 sinx+cosx=2cosx-2sinx,
sinx+cosx=2cosx-2sinx, ∴cosx=3sinx
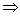 tanx=
tanx=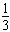
∴
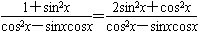
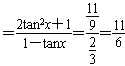 。
。
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
