题目内容
三棱柱ABC-A′B′C′的所有棱长都相等,侧棱与底面垂直,则异面直线BA1与AC1所成角的余弦值等于
.
| 1 |
| 4 |
| 1 |
| 4 |
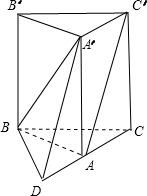
分析:延长CA到D,使AD=AC,根据异面直线所成角的定义可知∠DA′B就是异面直线BA′与AC′所成的角,解△A′DB,利用余弦定理可求得此角的余弦值.
解答:解:延长CA到D,使得AD=AC,则ADA′C′为平行四边形,
∴AC′∥A′D,∴∠DA′B就是异面直线BA′与AC′所成的角,
又三角形ABC为等边三角形,
设AB=AA′=1,
则BD=
=
;A′B=A′D=
,∠BAD=120°,
在△A′BD中,cos∠DA′B=
=
.
故答案是:
.
∴AC′∥A′D,∴∠DA′B就是异面直线BA′与AC′所成的角,
又三角形ABC为等边三角形,
设AB=AA′=1,
则BD=
1+1-2×1×1×(-
|
| 3 |
| 2 |
在△A′BD中,cos∠DA′B=
| 2+2-3 | ||||
2×
|
| 1 |
| 4 |
故答案是:
| 1 |
| 4 |

点评:本小题主要考查直三棱柱ABC-A′B′C′的性质、异面直线所成的角、异面直线所成的角的求法,考查转化思想.求异面直线所成的角,一般有两种方法,法一几何法,即利用“作、证、求”求得角;法二向量法,即利用向量的数量积公式求向量的夹角的余弦值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在三棱柱ABC-A′B′C′中,侧面CBB′C′⊥底面ABC,∠B′BC=60°,
在三棱柱ABC-A′B′C′中,侧面CBB′C′⊥底面ABC,∠B′BC=60°,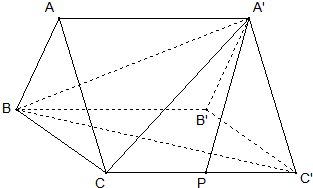 如图,正三棱柱ABC-A′B′C′中,
如图,正三棱柱ABC-A′B′C′中,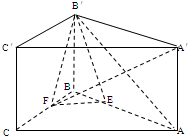 如图,在直三棱柱ABC-A′B′C′中,AB=BC=BB′=a,∠ABC=90°,点E、F分别是棱AB、BC上的动点,且AE=BF.
如图,在直三棱柱ABC-A′B′C′中,AB=BC=BB′=a,∠ABC=90°,点E、F分别是棱AB、BC上的动点,且AE=BF. (Ⅰ)求直三棱柱ABC-A′B′C′的体积;
(Ⅰ)求直三棱柱ABC-A′B′C′的体积;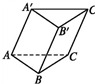 如图,斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为b,侧棱AA′与底面相邻两边AB,AC都成45°角.
如图,斜三棱柱ABC-A′B′C′中,底面是边长为a的正三角形,侧棱长为b,侧棱AA′与底面相邻两边AB,AC都成45°角.