题目内容
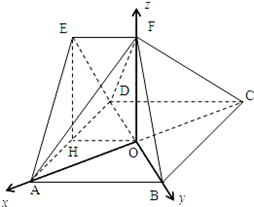
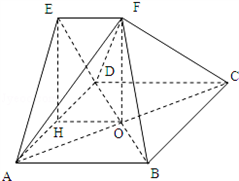
如图,在多面体ABCD﹣EF中,四边形ABCD为正方形,EF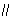 AB,EF⊥EA,AB=2EF,
AB,EF⊥EA,AB=2EF,
∠AED=90°,AE=ED,H为AD的中点.
(Ⅰ)求证:EH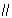 平面FAC;
平面FAC;
(Ⅱ)求证:EH⊥平面ABCD;
(Ⅲ)求二面角A﹣FC﹣B的大小.
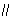 AB,EF⊥EA,AB=2EF,
AB,EF⊥EA,AB=2EF,∠AED=90°,AE=ED,H为AD的中点.
(Ⅰ)求证:EH
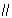 平面FAC;
平面FAC;(Ⅱ)求证:EH⊥平面ABCD;
(Ⅲ)求二面角A﹣FC﹣B的大小.
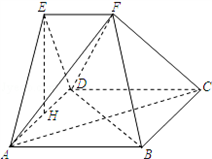
(Ⅰ)证明:AC∩BD=O,连接HO,FO
因为ABCD为正方形,所以O是AC中点,
又H是AD中点,
所以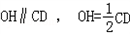 ,
,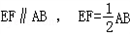 ,
,
所以EF∥OH且EF=OH,
所以四边形EHOF为平行四边形,
所以EH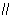 FO,
FO,
又因为FO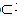 平面FAC,EH
平面FAC,EH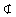 平面FAC.
平面FAC.
所以EH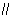 平面FAC.
平面FAC.
(Ⅱ)证明:因为AE=ED,H是AD的中点,
所以EH⊥AD
又因为AB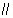 EF,EF⊥EA,所以AB⊥EA
EF,EF⊥EA,所以AB⊥EA
又因为AB⊥AD,所以AB⊥平面AED,
因为EH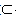 平面AED,
平面AED,
所以AB⊥EH,
所以EH⊥平面ABCD.
(Ⅲ)解:AC,BD,OF两两垂直,建立如图所示的坐标系,
设EF=1,则AB=2,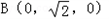 ,
, ,F(0,0,1)
,F(0,0,1)
设平面BCF的法向量为 ,
,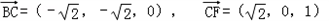 ,
,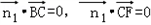
所以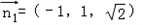
平面AFC的法向量为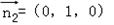
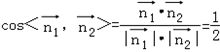 .
.
二面角A﹣FC﹣B为锐角,
所以二面角A﹣FC﹣B等于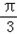 .
.
因为ABCD为正方形,所以O是AC中点,
又H是AD中点,
所以
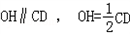 ,
,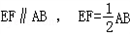 ,
,所以EF∥OH且EF=OH,
所以四边形EHOF为平行四边形,
所以EH
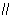 FO,
FO,又因为FO
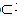 平面FAC,EH
平面FAC,EH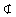 平面FAC.
平面FAC.所以EH
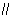 平面FAC.
平面FAC.(Ⅱ)证明:因为AE=ED,H是AD的中点,
所以EH⊥AD
又因为AB
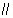 EF,EF⊥EA,所以AB⊥EA
EF,EF⊥EA,所以AB⊥EA又因为AB⊥AD,所以AB⊥平面AED,
因为EH
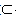 平面AED,
平面AED,所以AB⊥EH,
所以EH⊥平面ABCD.
(Ⅲ)解:AC,BD,OF两两垂直,建立如图所示的坐标系,
设EF=1,则AB=2,
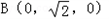 ,
, ,F(0,0,1)
,F(0,0,1)设平面BCF的法向量为
 ,
,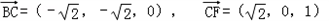 ,
,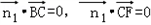
所以
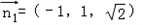
平面AFC的法向量为
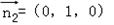
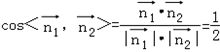 .
. 二面角A﹣FC﹣B为锐角,
所以二面角A﹣FC﹣B等于
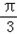 .
.

练习册系列答案
相关题目
 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC, (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC, (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=