题目内容
设点P是椭圆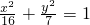 上的一动点,F是椭圆的左焦点,则|PF|的取值范围为________.
上的一动点,F是椭圆的左焦点,则|PF|的取值范围为________.
[1,7]
分析:设P(x0,y0),根据椭圆的第二定义可得 =
= ,即|PF|=
,即|PF|= +4,由此即可确定|PF|的取值范围.
+4,由此即可确定|PF|的取值范围.
解答:椭圆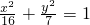 的左准线方程为
的左准线方程为
设P(x0,y0),则根据椭圆的第二定义可得 =
=
∴|PF|= +4
+4
∵-4≤x0≤4
∴
∴1≤ +4≤7
+4≤7
∴1≤|PF|≤7
故答案为:[1,7]
点评:本题考查椭圆的性质,考查椭圆的第二定义,解题的关键是表达出焦半径.
分析:设P(x0,y0),根据椭圆的第二定义可得
 =
= ,即|PF|=
,即|PF|= +4,由此即可确定|PF|的取值范围.
+4,由此即可确定|PF|的取值范围.解答:椭圆
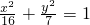 的左准线方程为
的左准线方程为
设P(x0,y0),则根据椭圆的第二定义可得
 =
=
∴|PF|=
 +4
+4∵-4≤x0≤4
∴

∴1≤
 +4≤7
+4≤7∴1≤|PF|≤7
故答案为:[1,7]
点评:本题考查椭圆的性质,考查椭圆的第二定义,解题的关键是表达出焦半径.

练习册系列答案
相关题目
 上的一动点,F是椭圆的左焦点,
上的一动点,F是椭圆的左焦点, 的取值范围为
.
的取值范围为
.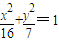 上的一动点,F是椭圆的左焦点,则|PF|的取值范围为 .
上的一动点,F是椭圆的左焦点,则|PF|的取值范围为 . 上的一动点,F是椭圆的左焦点,则|PF|的取值范围为( )
上的一动点,F是椭圆的左焦点,则|PF|的取值范围为( )