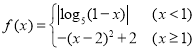题目内容
【题目】已知函数f（x）＝x
，且此函数图象过点（1，2）．
（1）求实数m的值；
（2）判断函数f（x）的奇偶性并证明；
（3）讨论函数f（x）在（0，1）上的单调性，并证明你的结论．
【答案】（1）m＝1（2）函数是奇函数,证明见解析（3）函数是单调递减函数,证明见解析
【解析】
（1）利用函数f（x）＝x
，且此函数图象过点（1，2），代入计算求实数m的值；
（2）利用函数f（x）的奇偶性的定义，判断与证明；
（3）利用定义证明函数f（x）在（0，1）上的单调性．
（1）∵函数f（x）＝x，且此函数图象过点（1，2），
∴2＝1+m，
∴m＝1；
（2）f（x）＝x
，定义域为：
，
又f（﹣x）＝﹣x
f（x），
∴函数f（x）是奇函数；
（3）函数f（x）在（0，1）上单调递减，
设0＜x1＜x2＜1，
则
，
∵0＜x1＜x2＜1，
∴x1﹣x2＜0，0＜x1x2＜1，x1x2﹣1＜0，
∴
，
即f（x1）＞f（x2），
∴f（x）在（0，1）上的单调递减．
练习册系列答案
相关题目
