Question

设函数

f(x)＝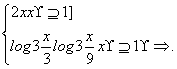

(1)求f(log₂ )与f(log )的值；

(2)求满足f(x)＝2的x的值；

(3)求f(x)的最小值．

Answer 1

解：(1)∵log₂ <log₂ 2＝1，

∴f(log₂ )＝2－log₂＝2log₂＝.

∵log ＝log()³＝3>1，

∴f(log )＝f(3)＝log₃ ·log₃ ＝log₃ 1·log₃ 3^－1＝0×(－1)＝0.

故f(log₂ )与f(log )的值分别为，0.

(2)当x≤1时，f(x)＝2^－x＝2，解得x＝－1，符合题意，当x>1时，f(x)＝log₃ ·log₃ ＝2

即(log₃x－1)(log₃x－2)＝2，

∴logx－3log₃x＝0，

∴log₃x＝3或log₃x＝0.

由log₃x＝0得x＝1，不合题意(舍去)．

由log₃x＝3，得x＝3³＝27>1符合题意．

综上可知，所求x的值为－1或27.

(3)当x≤1时，f(x)＝2^－x＝()^x≥()¹，

即f(x)_min＝.

当x>1时，f(x)＝(log₃x－1)(log₃x－2)．

令log₃x＝t，则t>0，

∴y＝(t－1)(t－2)＝(t－)²－，

∴当t＝>0时，y_min＝－<.

∴f(x)的最小值为－.