题目内容
a=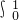 (2x+1)dx=________.
(2x+1)dx=________.
2
分析:欲求∫01(2x+1)dx,只须根据定积分的定义先求出被积函数的原函数,然后求解即可.
解答:a=∫01(2x+1)dx
=(x2+x)|01
=1+1
=2.
故答案为:2.
点评:本题主要考查了定积分,定积分运算是求导的逆运算,属于基础题.
分析:欲求∫01(2x+1)dx,只须根据定积分的定义先求出被积函数的原函数,然后求解即可.
解答:a=∫01(2x+1)dx
=(x2+x)|01
=1+1
=2.
故答案为:2.
点评:本题主要考查了定积分,定积分运算是求导的逆运算,属于基础题.

练习册系列答案
相关题目
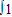 (2x+1)dx= .
(2x+1)dx= .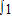 (2x+1)dx= .
(2x+1)dx= .