题目内容
如图所示,在半径为1的⊙O中,引两条互相垂直的直径AE和BF,在EF上取点C,弦AC交BF于P,弦CB交AE于Q,弦EF交AC于D.
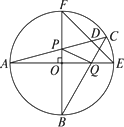
证明:四边形APQB的面积是1.
答案:
解析:
解析:
|
证明:因为AE、BF为互相垂直的两条直径,垂足O为圆心, 所以AE、BF互相平分,垂直且相等, 所以四边形ABEF是正方形. 所以∠ACB=∠AEF=45°,即∠DCQ=∠QED. 所以D、Q、E、C四点共圆. 连结CE、DQ, 则∠DCE+∠DQE=180°. 因为AE为⊙O的直径, 所以∠DCE=90°,∠DQE=90°. 因为∠FOE=90°, 进而DQ∥BF, 所以S△BPQ=S△BPD. 所以S△ABP+S△BPQ=S△ABP+S△BPD, 即S四边形ABQP=S△ABD. 因为⊙O的半径为1, 所以正方形边长为2, 即AB=AF=2. 所以S四边形ABQP=S△ABD= 分析:由已知条件可以证明四边形ABEF是正方形,且边长为 |

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 的正方形ABCD,向半圆内任投一点,求该点落在正方形内的概率.
的正方形ABCD,向半圆内任投一点,求该点落在正方形内的概率.
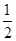 的正方形ABCD,向半圆内任投一点,则点落在正方形内的概率为________.
的正方形ABCD,向半圆内任投一点,则点落在正方形内的概率为________.

