题目内容
13.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,经过点F作倾斜角为135°的直线l交椭圆于A,B两点,线段AB的中点为M,直线AB与OM的夹角为θ,且tanθ=3,求这个椭圆的离心率.分析 设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0).kAB=-1.代入椭圆方程并且相减可得:$\frac{{y}_{0}}{{x}_{0}}$=$\frac{{b}^{2}}{{a}^{2}}$=kOM,由于直线AB与OM的夹角为θ,且tanθ=3,利用“到角公式”,解得kOM,再利用离心率计算公式即可得出.
解答 解:设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0),kAB=-1.
代入椭圆方程可得:$\frac{{x}_{1}^{2}}{{a}^{2}}+\frac{{y}_{1}^{2}}{{b}^{2}}$=1,$\frac{{x}_{2}^{2}}{{a}^{2}}+\frac{{y}_{2}^{2}}{{b}^{2}}$=1,
两式相减可得:$\frac{{x}_{0}}{{a}^{2}}-\frac{{y}_{0}}{{b}^{2}}$=0,
∴$\frac{{y}_{0}}{{x}_{0}}$=$\frac{{b}^{2}}{{a}^{2}}$=kOM,
∵直线AB与OM的夹角为θ,且tanθ=3,
∴3=$\frac{{k}_{OM}-(-1)}{1-{k}_{OM}}$,解得kOM=$\frac{1}{2}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,
∴这个椭圆的离心率e=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了椭圆的标准方程及其性质、“点差法”、“到角公式”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
1.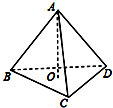 在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )
在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )
 在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )
在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )| A. | 三条中线的交点 | B. | 三角平分线的交点 | ||
| C. | 三条高线的交点 | D. | 三垂直平分线的交点 |
 如图,△ACB,△ADC都为等腰直角三角形,M、O为AB、AC的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2.
如图,△ACB,△ADC都为等腰直角三角形,M、O为AB、AC的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2.