题目内容
过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为（ ）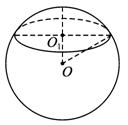
A.
B.
C.
D.
解析：设截面圆心为O1，半径为r,球半径为R,则r=
R,截面面积S1=π×(R)2=πR2.
球的表面积S=4πR2.
∴=.
答案：A
练习册系列答案
阅读快车系列答案
相关题目
过球的一条半径的中点作垂直于这条半径的球的截面，则此截面面积是球表面积的（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
（B）
（C）
（D）
B.
C.
D.