题目内容
已知点P是抛物线y2=4x上的一点,F为抛物线的焦点,A(3,1),求|PA|+|PF|的最小值和此时P的坐标.
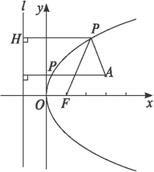
思路解析：数形结合,将|PF|转化为P到其准线的距离,找到最值状态. 解：如图所示.设抛物线的准线为l,作PH⊥l于H,则|PH|=|PF|, ∴|PA|+|PF|=|PH|+|PA|. ∴当且仅当A、P、H三点共线，即PA⊥l时，|PA|+|PF|取得最小值. 又A到l的距离是4，则（|PA|+|PF|）min=4，此时P的坐标是（ ∴当P的坐标是（ 深化升华 当A在抛物线“内部”时，|PA|+|PF|的最小值是A到准线的距离；当A在抛物线上或其“外部”时，|PA|+|PF|的最小值是|AF|. 直线与抛物线仅有一个公共点时，直线与抛物线未必相切，也可能直线平行于轴.
，1）.
，1）时，|PA|+|PF|取最小值4.
练习册系列答案
赢在课堂激活思维系列答案
金考卷单元专项期中期末系列答案
步步高大一轮复习讲义系列答案
毕业生暑期必读系列答案
名师金手指暑假生活系列答案
暑假乐园星球地图出版社系列答案
名校秘题全程导练系列答案
新锐图书假期园地暑假作业中原农民出版社系列答案
暑假百分百期末暑假衔接总复习系列答案
相关题目
已知点P是抛物线y2=2x上的动点，点P在y轴上的射影是M，点A(
，4)，则|PA|+|PM|的最小值是（ ）
| 7 |
| 2 |
| A、5 | ||
B、
| ||
| C、4 | ||
| D、AD |