题目内容
如图,在梯形ABCD中,|AB|=2|CD|,点E分有向线段
分析:建立坐标,由双曲线的性质及定比分点公式等建立λ与e之间的关系.
解:以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xOy,所以A(-c,0)(其中c=![]() |AB|为双曲线
|AB|为双曲线![]() -
-![]() =1,a>0的半焦距),xC=
=1,a>0的半焦距),xC=![]() ,由定比分点坐标公式,得
,由定比分点坐标公式,得
xE=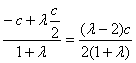 .
.
由双曲线的焦半径公式,得|AC|=exC+a=![]() +a,
+a,
|AE|=-exE-a=-![]() -a.
-a.
又![]() =
=![]() ,∴
,∴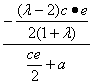 =
=![]() .
.
解之得e2=![]() =-2+
=-2+![]() .
.
由![]() ≤λ≤
≤λ≤![]() ,∴7≤e2≤10,即
,∴7≤e2≤10,即![]() ≤e≤
≤e≤![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
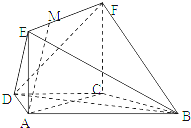 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.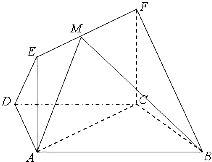 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.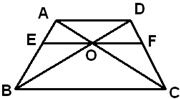 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.