题目内容
某少数民族的刺绣有着悠久的历史,右图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5);
(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的表达式;
(3)求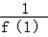 +
+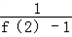 +
+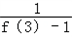 +…+
+…+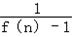 的值.
的值.
(1)求出f(5);
(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的表达式;
(3)求
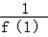 +
+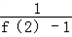 +
+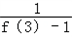 +…+
+…+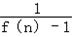 的值.
的值.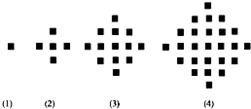
解:(1)∵f(1)=1,
f(2)=1+4=5,
f(3)=1+4+8=13,
f(4)=1+4+8+12=25,
∴f(5)=1+4+8+12+16=41.
(2)∵f(2)﹣f(1)=4=4×1,
f(3)﹣f(2)=8=4×2,
f(4)﹣f(3)=12=4×3,
f(5)﹣f(4)=16=4×4,
由上式规律得出f(n+1)﹣f(n)=4n.
∴f(n)﹣f(n﹣1)=4(n﹣1), f(n﹣1)﹣f(n﹣2)=4 (n﹣2), f(n﹣2)﹣f(n﹣3)=4
(n﹣2), f(n﹣2)﹣f(n﹣3)=4 (n﹣3), … f(2)﹣f(1)=4×1,
(n﹣3), … f(2)﹣f(1)=4×1,
∴f(n)﹣f(1)=4[(n﹣1)+(n﹣2)+…+2+1] =2(n﹣1) n,
n,
∴f(n)=2n2﹣2n+1.
(3)当n≥2时,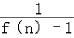 =
=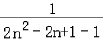 =
=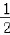 (
(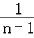 ﹣
﹣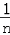 ),
),
∴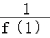 +
+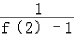 +
+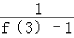 +…+
+…+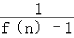
=1+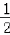 (1﹣
(1﹣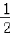 +
+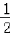 ﹣
﹣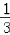 +…+
+…+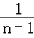 ﹣
﹣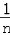 )
)
=1+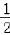 (1﹣
(1﹣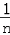 )=
)=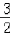 ﹣
﹣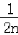 .
.
f(2)=1+4=5,
f(3)=1+4+8=13,
f(4)=1+4+8+12=25,
∴f(5)=1+4+8+12+16=41.
(2)∵f(2)﹣f(1)=4=4×1,
f(3)﹣f(2)=8=4×2,
f(4)﹣f(3)=12=4×3,
f(5)﹣f(4)=16=4×4,
由上式规律得出f(n+1)﹣f(n)=4n.
∴f(n)﹣f(n﹣1)=4(n﹣1), f(n﹣1)﹣f(n﹣2)=4
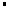 (n﹣2), f(n﹣2)﹣f(n﹣3)=4
(n﹣2), f(n﹣2)﹣f(n﹣3)=4 (n﹣3), … f(2)﹣f(1)=4×1,
(n﹣3), … f(2)﹣f(1)=4×1,∴f(n)﹣f(1)=4[(n﹣1)+(n﹣2)+…+2+1] =2(n﹣1)
 n,
n,∴f(n)=2n2﹣2n+1.
(3)当n≥2时,
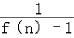 =
=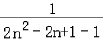 =
=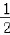 (
(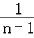 ﹣
﹣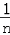 ),
),∴
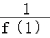 +
+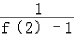 +
+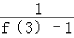 +…+
+…+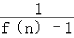
=1+
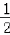 (1﹣
(1﹣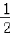 +
+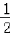 ﹣
﹣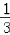 +…+
+…+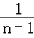 ﹣
﹣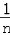 )
)=1+
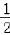 (1﹣
(1﹣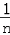 )=
)=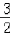 ﹣
﹣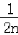 .
.
练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目


 某少数民族的刺绣有着悠久的历史,右图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,右图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形. 某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形. 个图形包含
个图形包含 个小正方形,则
个小正方形,则
