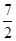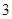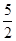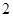题目内容
若点A的坐标为(3,2),F为抛物线y2=2x的焦点,点P是抛物线上的一动点,则|PA|+|PF|取得最小值时点P的坐标是( )
| A.(0,0) | B.(1,1) | C.(2,2) | D.(
|
根据题意,作图如下,

设点P在其准线x=-
上的射影为M,有抛物线的定义得:|PF|=|PM|,
∴欲使|PA|+|PF|取得最小值,就是使|PA|+|PM|最小,
∵|PA|+|PM|≥|AM|(当且仅当M,P,A三点共线时取“=”),
∴|PA|+|PF|取得最小值时(M,P,A三点共线时)点P的纵坐标y0=2,设其横坐标为x0,
∵P(x0,2)为抛物线y2=2x上的点,
∴x0=2,
∴点P的坐标为P(2,2).
故选C.

设点P在其准线x=-
| 1 |
| 2 |
∴欲使|PA|+|PF|取得最小值,就是使|PA|+|PM|最小,
∵|PA|+|PM|≥|AM|(当且仅当M,P,A三点共线时取“=”),
∴|PA|+|PF|取得最小值时(M,P,A三点共线时)点P的纵坐标y0=2,设其横坐标为x0,
∵P(x0,2)为抛物线y2=2x上的点,
∴x0=2,
∴点P的坐标为P(2,2).
故选C.

练习册系列答案
相关题目
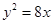 的焦点为F,准线为
的焦点为F,准线为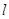 ,P是
,P是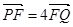 ,则
,则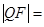 ( )
( )